水电站课设(二)

2024.6.23 好久不见。 第六学期的考试正式结束，意味着小学期的课设正式开始。水电站课程设计的任务在十天前已经下发，现在来做一个总结。 ## 使用数据

计算期初水位：173.45 优化调度最小下泄流量：4690 比较年份：1949

新任务

提取各时段的运行规则。根据水库优化调度模型求解结果，提取各时段的调度规则。

问题分析

-- 使用的数据是水库优化调度模型所得到的求解结果 -- 目前需要首先重新修正优化调度模型，修正结果，增加数据结果，形成数据总表

代码改进

在阅读文献的时候没有发现有设置汛期水位完全不变的情况，故现在对结课设计进行改变，取消汛期水位限制。另外需要将所有约束条件放入if内，修正递推函数。

目前决定重新编制优化调度代码，首先列出约束条件、初始值、递推函数，预计明天完善完成。代码如下：

代码一

%%水库优化调度代码（第二版）
%确定初始值及数据结构
V(1) = 377.45;%计算初始库容
Z(1) = 175;%计算初始水位
Pb = 499;%保证出力
%设决策变量为下泄流量Qfd(t,1),可能出现弃水Qqs(t,1)
%%约束条件编制
%发电水头约束
H(t) = head(Qxx,hsy);%输入下泄流量及上游水头
%水电站预想出力限制
yxcl(t) = Yuxcl(H(t));%输入当前水头
%水电站最大过流能力限制
xxnl(t) = Xiaxnl(hsy);%输入当前上游水位
%生态流量限制
Qst = input("最小生态流量为");%本次计算为5690
%水量平衡约束
V(t+1) = V(t)+(Qrk(t)-Qfd(t)-Qqs(t))*T(t);
%库容曲线约束
Z(t+1) = Kurqx(V(t+1));%当前时段末库容
%库水位约束
Z(t) >= 145;
Z(t) <= 185;
%初末库水位约束
Z(1) = 175;
Z(36) = 175;

%指标函数
P(t) = k*Qfd(t)*H(t);
if P(t) > Pb
    P(t) = P(t);
else
    P(t) = P(t) + b*(P(t)-Pb);%b为惩罚系数
end

%%递推函数
SumP(t) = max(P(t)+SumP(t+1));

---

今日任务

处理状态和决策离散化与时段平均出力的计算方法和具体代码。

进度

基本完成代码编制，但是数据意义还需要思考，另需要正确获取最优解的数值。

新知识点

max函数意为返回数组的最大值。

明日任务

完成动态规划代码修改

---

进度

昨晚进行到需要在已得到数据中提取需要的最优解的一组数据，但收工后思考之后发现，如果按照真正计算出来的所有结果来选择最优解，就失去了所谓动态规划面向时段的优势和意义，即无视了动态规划的性质——最优解的每个局部解也都是最优的。

故现在开始思考，为什么课本上和课堂上老师都在强调逆推过程而不是更加符合时间顺序的顺推过程？目前我认为，逆推时后一时段的水位和面临时段的来流可以看作八个约束条件之一，每一个时段的计算都是已知结果通过下泄流量来确定上一时段的库容和水位，依此找到确定结果的放水过程的最优解。

结论&任务

上述思想可行且所得到的结果效果很好，和结果设计版本相比有较大的完善。在结课作业中尚有一项未能完成，即惩罚因子的大小和保证率的关系。接下来寻找一下二者的函数关系。

结论

没有找到关系☹️

现附所有动态规划代码如下：

代码二

%%水库优化调度代码（第二版）
%确定初始值及数据结构
n = 36;%计算时段数
Vmin = 171.5;
Vmax = 505;
Z = zeros(36,1000);
V = zeros(36,1000);
V(36,:) = 377.45;
V(1,:) = 377.45;
Z(1,:) = 175;
Z(36,:) = 175;%计算初始水位
Pb = 499;%保证出力
P = zeros(36,1000);
SumP = 0;
T = 10*3600*24/100000000;%各时段时间间隔

%设决策变量为下泄流量Qfd(t,1),可能出现弃水Qqs(t,1)
%生态流量限制
Qst = 5690;%本次计算为5690

%%单时段离散化与平均出力的计算方法
%将一时段的状态V(t)离散为M个数值
%又水库水位限制为(145,185)
%故首先选择将水库库容离散为40个数值（即一米一个库容）
%又首先需要确定Qfd的离散值
%故制作Qfd初始值表格
%表格范围设置为（生态流量，时段最大下泄流量）
%此次计算设Qfd为决策变量
b = linspace(0,1,100);
%b = 0.8;

for k = 1:1000
flag = 0;

for j = 1:35

t = n-j;
%
if t == 1
    i = 1;
    Qxx(t,i) = abs(Qrk(t,1) - (V(t+1,1) - V(t,1))/T);
     %库容曲线约束
     Z(t,i) = Kurqx(V(t,i));%当前时段末库容
     %发电水头约束
     [H(t+1,i),kcl(t,i)] = head(Qxx(t,i),Z(t,i));%输入下泄流量及上游水头
     %时段平均出力
     P(t+1,:) = kcl(t,i)*Qxx(t,i)*H(t,i)/10000;
     Pmax(t+1,i) = P(t+1,i);
     h(t+1,i) = H(t+1,i);
     break;
else
%}
for i = 1:1000
%水电站最大过流能力限制
    xxnl(t) = Xiaxnl(Z(t+1,i));%输入当前上游水位,计算当前时段水库最大下泄能力
    Qfd = linspace(Qst,xxnl(t),1000);%Qfd初始数组，共1000个数据点
    
            V(t,i) = V(t+1,i) - (Qrk(t+1,1)-Qfd(i))*T;
            
            if V(t,i) < Vmin
                V(t,i) = Vmin;
                Qxx(t+1,i) = abs(Qrk(t+1,1) - (V(t+1) - V(t))/T);
    
            %库容曲线约束
            Z(t,i) = Kurqx(V(t,i));%当前时段末库容
            %发电水头约束
            [H(t+1,i),kcl(t+1,i)] = head(Qxx(t+1,i),Z(t,i));%输入下泄流量及上游水头
            if H(t+1,i) < 0
                continue;%继续i循环
            end
            %时段平均出力
            P(t+1,i) = kcl(t+1,i)*Qxx(t+1,i)*H(t+1,i)/10000;
            %水电站预想出力限制
            yxcl(t+1,i) = Yuxcl(H(t+1,i));%输入当前水头
    
            continue;%跳出i循环
    
            elseif V(t,i) > Vmax
                Qqs(t+1,i) = (V(t,i)-Vmax)/T;
                V(t,i) = Vmax;
                Qxx(t+1,i) = abs(Qrk(t+1,1) - (V(t,i) - V(t+1,i))/T);
            else
                Qxx(t+1,i) = Qfd(i);
            end
           
            %库容曲线约束
            Z(t,i) = Kurqx(V(t,i));%当前时段末库容
            %发电水头约束
            [H(t+1,i),kcl(t+1,i)] = head(Qxx(t+1,i),Z(t,i));%输入下泄流量及上游水头
            %时段平均出力
            if H(t+1,i) < 0
                continue;
            end
            P(t+1,i) = kcl(t+1,i)*Qxx(t+1,i)*H(t+1,i)/10000;
            %水电站预想出力限制
            yxcl(t+1,i) = Yuxcl(H(t+1,i));%输入当前水头


            %%指标函数
            %
            if P(t,i) > yxcl(t)
                P(t,i) = yxcl(t);
                %flag(t) = 1;
            %}
            elseif P(t+1,i) > Pb && P(t,i) < yxcl(t)
                P(t+1,i) = P(t+1,i);
                %flag(t) = 1;
            else
                P(t+1,i) = P(t+1,i) + b(1,k)*(P(t+1,i)-Pb);%b为惩罚系数
            end
end
%
for f = 1:999
    if P(t+1,f) > P(t+1,f+1)
        Ppro(t+1,f) = P(t+1,f);   
    end
end
[Pmax(t+1,1),l] = max(Ppro(t+1,1:200));
V(t,:) = V(t,l);
Z(t,:) = Z(t,l);
Q(t+1,1) = Qxx(t+1,l);
qs(t+1,1) = Qqs(t+1,l);
h(t+1,1) = H(t+1,l);


end
end

for m = 1:36
if Pmax(m,1) > Pb
    flag = flag+1;
end
end

per(k,1) = flag/36;
end

做出图像如下：

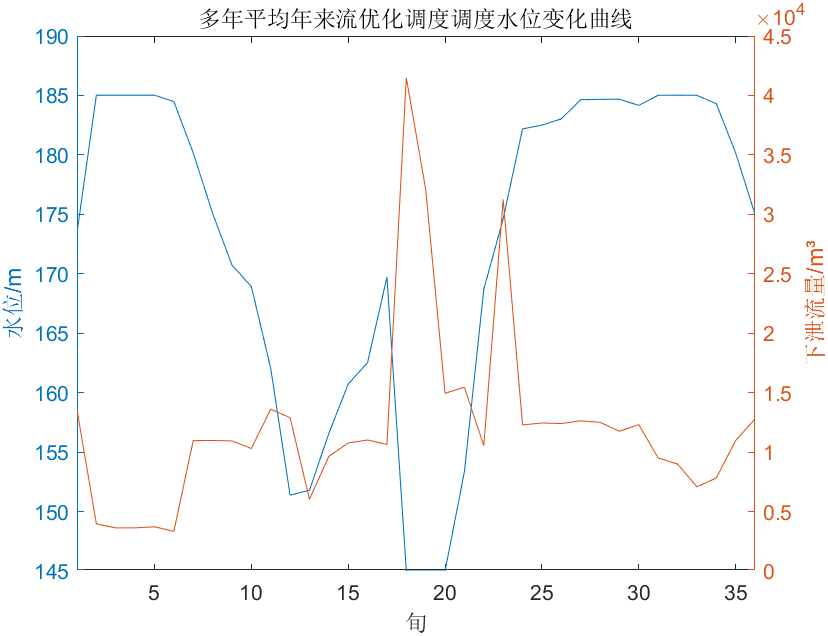
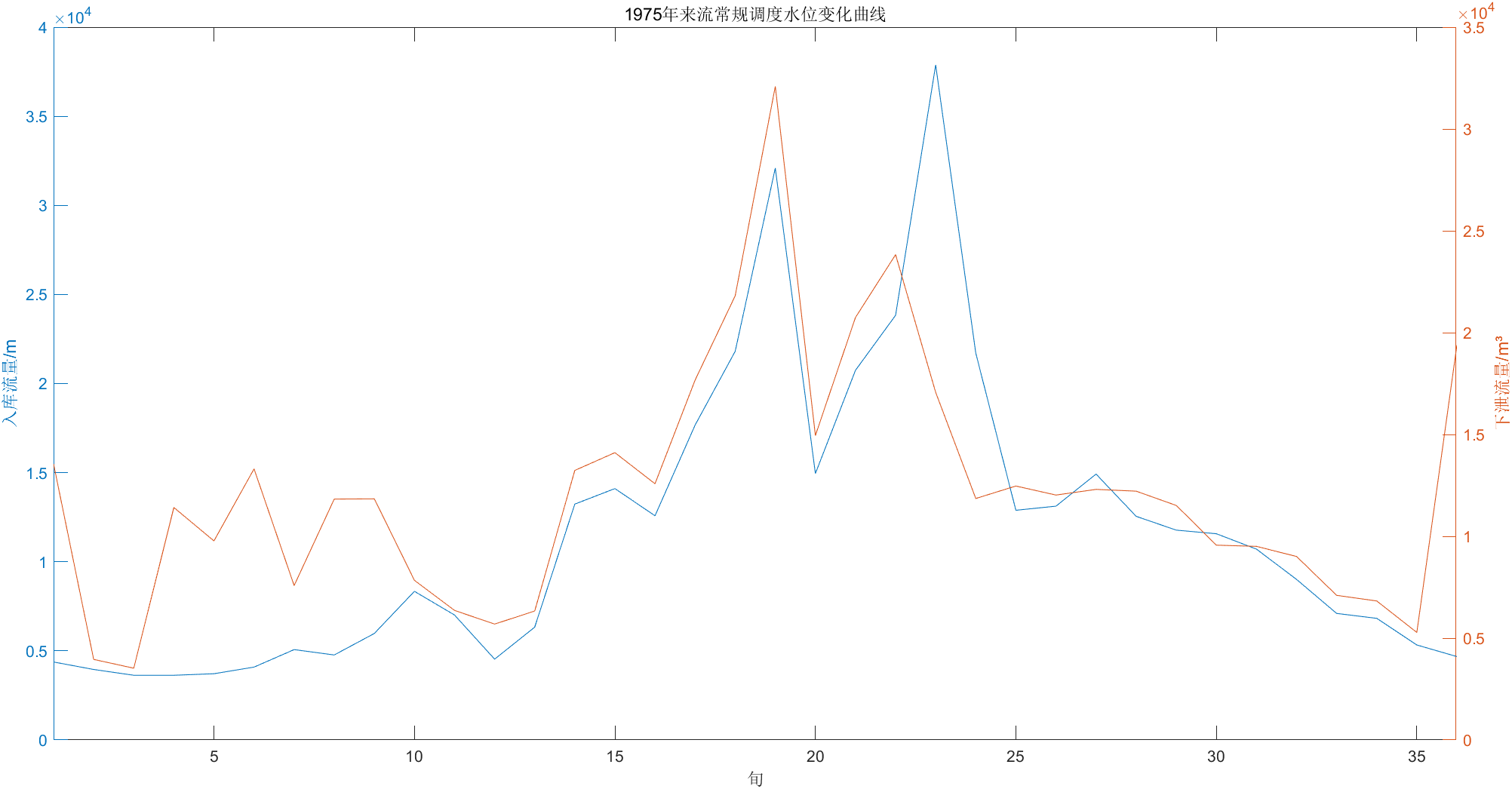
明日任务

读文献，基本得出函数关系式，基本确定编程思路，得出所有可以用于训练模型的数据。

---

读文献有感

• 具体阅读了有关NSGA-Ⅱ(Non-dominated Sorting Genetic Algorithm)的优化思路和实现方法，如果在课设报告提交前尚有时间，可以考虑把优化调度的方法从动态规划改变为NSGA。 [1] A Fast Non-dominated Sorting Genetic Algorithm For Multi-objective Optimization:NSGA-Ⅱ

• 粒子群优化算法（PSO）由鸟群寻找食物得到灵感，通过计算寻找“最好的”粒子，即“离食物最近的”粒子，因此可用于在已有优化调度数据的前提下拟合提取调度函数。

有一关键评价函数，优化适应度函数。用于评价每一个粒子的“好坏”，从而决定优化方向。

调度函数表达式

\[ Q_{t} = \alpha_{t} \cdot I_{t} + \beta_{t} \cdot _V{t} \]

其中，\(Q_{t}\) 为t时段下泄流量，\(I_{t}\) 为t时段入流，\(V_{t}\) 为t时段初库容.

matlab语法学习

1.函数句柄：在matlab中，函数可以像变量一样进行传递和操作。函数句柄就是指向函数的指针，可以调用函数或者将函数作为参数传递给其他函数。

2.@符号：在matlab中，@符号用于创建函数句柄。

PSO算法具体实现代码

http://t.csdnimg.cn/Xpizk

PSO算法

%pop——种群数量
%dim——问题维度
%ub——变量上界，[1,dim]矩阵
%lb——变量下界，[1,dim]矩阵
%fobj——适应度函数（指针）
%MaxIter——最大迭代次数
%Best_Pos——x的最佳值
%Best_Score——最优适应度
 

clc;
clear all;
close all;
pop=50;
dim=2;
ub=[10,10];
lb=[-10,-10];
vmax=[2,2];
vmin=[-2,-2];
maxIter=100;
fobj=@(X)fun(X);
[Best_Pos,Best_fitness,IterCurve]=pso(pop,dim,ub,lb,fobj,vmax,vmin,maxIter);
figure
plot(IterCurve,'r','linewidth',2);
grid on;
disp(['求解得到的x1，x2是:',num2str(Best_Pos(1)),' ',num2str(Best_Pos(2))]);
disp(['最优解对应的函数:',num2str(Best_fitness)]);


%%确定计算初始值 
function [X]=initialization(pop,ub,lb,dim)%得到在范围内的初始数据
    for i=1:pop
        for j=1:dim
            X(i,j)=(ub(j)-lb(j))*rand()+lb(j);%在限定的  
        end 
    end
end

function fitness=fun(x)
    fitness=sum(x.^2);
end

function [X]=BoundaryCheck(X,ub,lb,dim)%检查原始数据
    for i=1:dim
        if X(i)>ub(i)
            X(i)=ub(i);
        end
        if X(i)<lb(i)
            X(i)=lb(i);
        end
    end
end

%%PSO计算
function [Best_Pos,Best_fitness,IterCurve]=pso(pop,dim,ub,lb,fobj,vmax,vmin,maxIter)
c1=2.0;
c2=2.0;
V=initialization(pop,vmax,vmin,dim);
X=initialization(pop,ub,lb,dim);
fitness=zeros(1,pop);
for i=1:pop
    fitness(i)=fobj(X(i,:));
end
pBest=X;
pBestFitness=fitness;
[~,index]=min(fitness);
gBestFitness=fitness(index);
gBest=X(index,:);
Xnew=X;
fitnessNew=fitness;
for t=1:maxIter
    for i=1:pop
        r1=rand(1,dim);
        r2=rand(1,dim);
        V(i,:)=V(i,:)+c1.*r1.*(pBest(i,:)-X(i,:))+c2.*r2.*(gBest-X(i,:));
        V(i,:)=BoundaryCheck(V(i,:),vmax,vmin,dim);
        Xnew(i,:)=X(i,:)+V(i,:);
        fitnessNew(i)=fobj(Xnew(1,:));
        if fitnessNew(i)<pBestFitness(i)
            pBest(i,:)=Xnew(i,:);
            pBestFitness(i)=fitnessNew(i);
        end
        if fitnessNew(i)<gBestFitness
            gBestFitness=fitnessNew(i);
            gBest=Xnew(i,:);
        end
    end
    X=Xnew;
    fitness=fitnessNew;
    Best_Pos=gBest;
    Best_fitness=gBestFitness;
    IterCurve(t)=gBestFitness;
end
end

需要解决的问题

根据上述代码及文献，已经基本搞清楚PSO算法的编写过程和思路。现在需要解决的关键问题是如何设置变量内容、变量的数据结构和变量的上下界，即如何利用优化调度已经得到的数据通过PSO得到想要的参数拟合结果。

根据所找文献，他将参数按照月份进行了划分，将非汛期的每一月都进行了参数拟合计算。所以提出以下思路：

• 将每一月的入库流量和下泄流量作为输入参数，从1941-1990共50年，即初始种群数为50，先假设迭代次数为200。

• 按照文献已经得到的参数，假设需要得到的三个参数为“粒子的最优坐标”，即三维PSO问题。

明日任务

完成变量数据结构设计，初步完成PSO代码。

---

matlab语法学习

• num2str函数：将数字转换为字符数组

训练数据准备

按照列出的关系表达式，需要的初始数据有：当前时段的初始库容、时段入流，以及由优化调度得到的下泄流量。

依据文献所给思路，编制50年各旬下泄流量、初始库容、时段入流的数据表，即36个50×3列数据表。

训练数据使用

每一旬得到的三组数据用于拟合数据参数，相当于二元一次线性非齐次方程组求“最接近的解。对于PSO，初始搜索点的位置及速度一般是在允许的范围内随机产生的，而对于函数提取，初始点的数据即为优化调度已得到的数据。

类比可以推测，可以将时段入流和初始库容作为”初始搜索点“，即初始位置，将下泄流量作为速度。

接上述观点，既然PSO不需要初始值，是不是优化调度获得的数据其实并不能直接用于参数估计，而是作为变量范围作为参考，迭代次数增加其实是在更加逼近范围内的最优值，而最优值也是由优化调度过程给出的。所以PSO是作为反映优化调度规律，便于调度计算而使用的算法。

结果

现得到36组参数数据，还需要带入具体流量数据进行测试。

---

成果得出

最后得到由调度函数调度的水位变化曲线和下泄流量曲线。

修改的PSO算法代码如下：

PSO算法（修改版）

%pop——种群数量
%dim——问题维度
%ub——变量上界，[1,dim]矩阵
%lb——变量下界，[1,dim]矩阵
%fobj——适应度函数（指针）
%MaxIter——最大迭代次数
%Best_Pos——x的最佳值
%Best_Score——最优适应度
 
for i = 1:36 
    for j = 1:50
a = Data(j,3*i-1);
b = Data(j,3*i);
c = Data(j,3*i-2);
pop=50;
dim=2;
vmax=[max(Data(:,3*i-1)),max(Data(:,3*i))];
vmin=[min(Data(:,3*i-1)),min(Data(:,3*i))];
ub=[2,2];
lb=[0,0];
maxIter=2000;
fobj=@(X,a,b,c)fun(X,a,b,c);
[Best_Pos,Best_fitness,IterCurve]=pso(pop,dim,ub,lb,fobj,vmax,vmin,maxIter,a,b,c);
canshu(j,2*i-1) = Best_Pos(1);
canshu(j,2*i) = Best_Pos(2);
%{
figure
plot(IterCurve,'r','linewidth',2);
grid on;
disp(['求解得到的x1，x2是:',num2str(Best_Pos(1)),' ',num2str(Best_Pos(2))]);
disp(['最优解对应的函数:',num2str(Best_fitness)]);
%}
    end 
end
for i = 1:72    
    ave(i,1) = mean(canshu(:,i));
    %ave(2*i,2) = mean(canshu(:,2*i));
end

 
%初始化粒子坐标和粒子速度
function [X]=initialization(pop,ub,lb,dim)
    for i=1:pop
        for j=1:dim
            X(i,j)=(ub(j)-lb(j))*rand()+lb(j);%在限定的  
        end 
    end
end
 
function fitness=fun(x,a,b,c)
    fitness=sum(abs(c-x.*[a;b*100000000/(24*3600*10)]*[1;1]));
end

%检查初始数据点坐标位置是否在允许范围内
function [X]=BoundaryCheck(X,ub,lb,dim)
    for i=1:dim
        if X(i)>ub(i)
            X(i)=ub(i);
        end
        if X(i)<lb(i)
            X(i)=lb(i);
        end
    end
end
 
function [Best_Pos,Best_fitness,IterCurve]=pso(pop,dim,ub,lb,fobj,vmax,vmin,maxIter,a,b,c)
c1=2.0;
c2=2.0;
V=initialization(pop,vmax,vmin,dim);
X=initialization(pop,ub,lb,dim);
fitness=zeros(1,pop);
for i=1:pop
    fitness(i)=fobj(X(i,:),a,b,c);
end
pBest=X;
pBestFitness=fitness;
[~,index]=min(fitness);
gBestFitness=fitness(index);
gBest=X(index,:);
Xnew=X;
fitnessNew=fitness;
for t=1:maxIter
    for i=1:pop
        r1=rand(1,dim);
        r2=rand(1,dim);
        V(i,:)=V(i,:)+c1.*r1.*(pBest(i,:)-X(i,:))+c2.*r2.*(gBest-X(i,:));
        V(i,:)=BoundaryCheck(V(i,:),vmax,vmin,dim);
        Xnew(i,:)=X(i,:)+V(i,:);
        fitnessNew(i)=fobj(Xnew(1,:),a,b,c);
        if fitnessNew(i)<pBestFitness(i)
            pBest(i,:)=Xnew(i,:);
            pBestFitness(i)=fitnessNew(i);
        end
        if fitnessNew(i)<gBestFitness
            gBestFitness=fitnessNew(i);
            gBest=Xnew(i,:);
        end
    end
    X=Xnew;
    fitness=fitnessNew;
    Best_Pos=gBest;
    Best_fitness=gBestFitness;
    IterCurve(t)=gBestFitness;
end
end

根据所提取的调度函数进行时段计算的代码如下：

调度函数

%%利用调度函数调度(1949)
flag = 0;
T = 24*3600*10/100000000;
Vmax = 505;
Zmax = 185;
Vhs = zeros(36,1);
Vhs(1,1) = 377.45;
Zhs = zeros(36,1);
Zhs(1,1) = 173.45;
for t = 1:36
Qhs(t,1) = ave(2*t-1,1)*Qrk(t,1)+ave(2*t,1)*Vhs(t,1)/T;
Vhs(t+1,1) = Vhs(t,1) + (Qrk(t,1)-Qhs(t,1))*T;
if Vhs(t+1,1) > Vmax
    Qhsqs(t+1,1) = (Vhs(t+1,1) - Vmax)/T;
    Vhs(t+1,1) = Vmax;
    Zhs(t+1,1) = Zmax;
    Qhs(t,1) = Qrk(t,1)-(Vhs(t+1,1)-Vhs(t,1))/T;
end
%库容曲线约束
Zhs(t+1,1) = Kurqx(Vhs(t+1,1));%当前时段末库容
%发电水头约束
[Hhs(t,1),kclhs(t,1)] = head(Qhs(t,1),Zhs(t,1));%输入下泄流量及上游水头
Phs(t,1) = kclhs(t,1)*Qhs(t,1)*abs(Hhs(t,1)/10000);
end
for i = 1:36
    if Phs(i,1) > 499
        flag = flag + 1;
    end
end
per = flag/36;

yyaxis left
plot(1:37,Zhs(:,1));
xlim([0 36]);
ylim([145,190]);
ylabel("水位/m");
hold on
yyaxis right
plot(1:36,Qhs(:,1));
xlim([1,36]);
ylabel("下泄流量/m³");

xlabel("旬");
title("1949年来流调度函数水位变化曲线");

调度函数图像

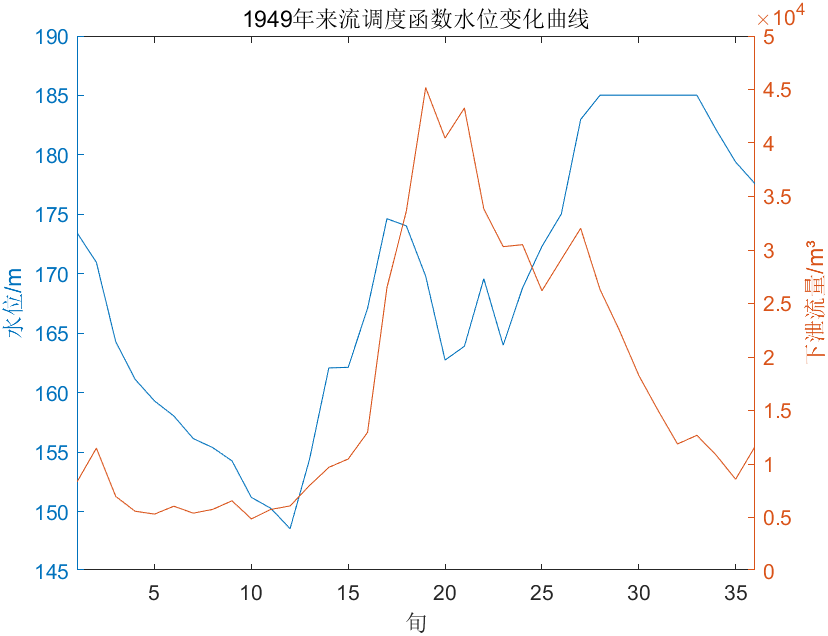
结果比较

根据得出的数据对常规调度、优化调度、调度函数调度进行比较。

选择比较的参数：平均水位、发电水头、下泄流量、弃水量、保证率和总发电量。

经比较可以发现，三种方法的平均水位，平均下泄流量和发电水头差别不大，调度函数调度弃水较多，而常规调度后期水位很高，但前期为了符合调度图调度发电量较低，其中优化调度的结果较为实用。

具体比较数据见下表。

	平均出力	保证率	平均水头	平均水位	平均下泄流量	弃水量
常规调度	431.59	55%	91.69	165.62	17364.8	0
优化调度	779.81	95%	55	166	17557.44	0
调度图	445.4	65%	57	168.77	17441.272	33039.45